Sobre los tipos de soluciones

Considere el siguiente problema:

Max. Z = 50X₁ + 6X₂

Sujeto a:

2X₁ + 8X₂ ≤ 4

5X₁ + 9X₂ ≥ 11

siendo además ambos procesos no negativos. La zona factible de la primera restricción es el semiplano que deja a su parte izquierda (sombreada en verde), mientras que para la segunda, esa zona factible es el semiplano superior (sombreado en azul); no hay ninguna zona de superposición, lo que significa que no hay ninguna combinación (X1, X2) que verifique simultáneamente las dos restricciones. El conjunto factible es vacío, y el problema carece de solución.

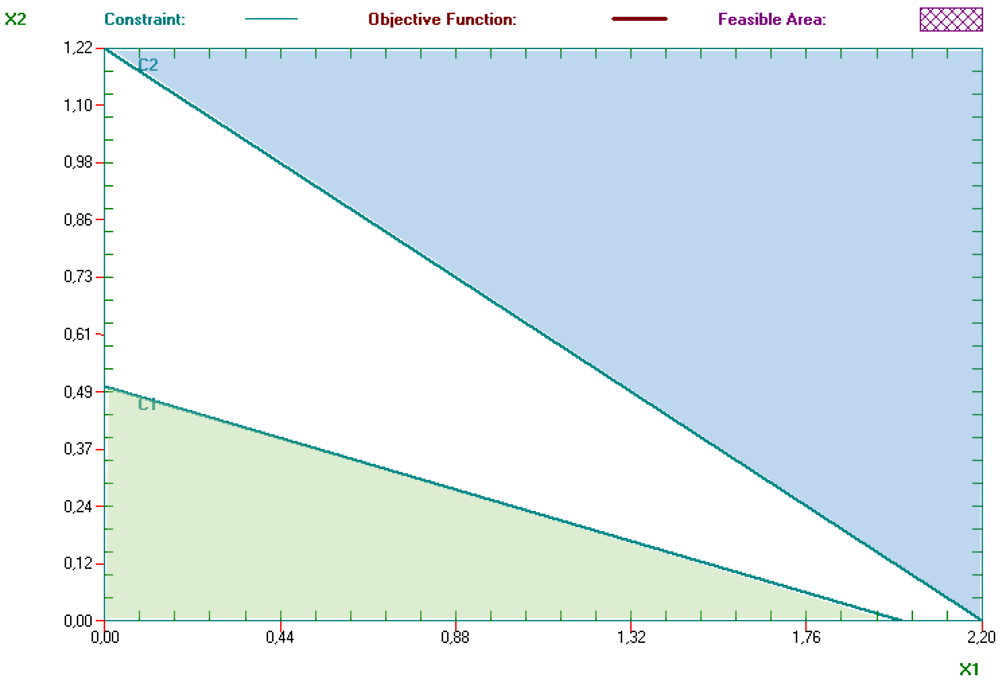
¿Qué hacer con un problema sin solución?

Un problema puede carecer de solución simplemente porque está mal especificado, o porque se han cometido errores en su formulación. Sin embargo la causa más común es que las restricciones son excesivamente rígidas: por ejemplo, si representan recursos limitados, la disponibilidad es insuficiente para atender un programa de producción satisfactorio. Lejos de representar un fracaso, este resultado nos ayuda a planificar las acciones correctoras necesarias: si observa el gráfico superior, puede intuir que la solución requeriría desplazar la primera restricción hacia arriba y/o la segunda hacia abajo: debe aumentar la disponibilidad del recurso 1 y/o reducir el nivel de exigencia para el segundo.

Por ejemplo, si logra que P1 = 5 y P2 = 10, puede establecer la siguiente solución:

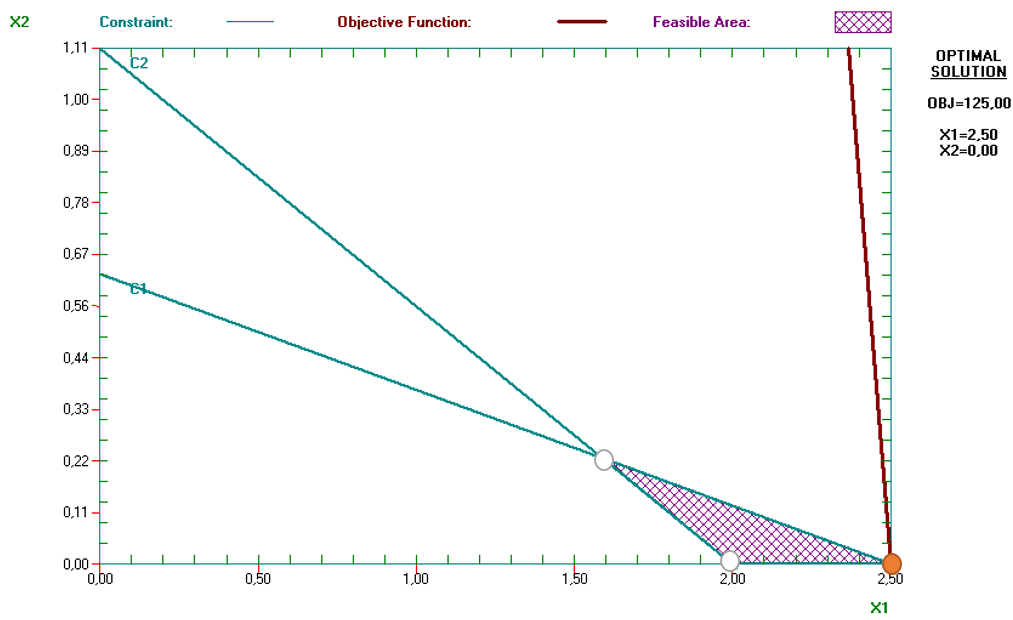
No olvide que hay otras posibilidades, además de cambiar los límites de las restricciones. En particular, podría tratar de reducir los coeficientes técnicos (los consumos de recursos por unidad de X1 y X2), es decir, incrementar la productividad. Esto no desplazaría las restricciones, sino que modificaría su pendiente, y presumiblemente nos permitiría también hallar soluciones factibles.

Para poder hallar una solución óptima es preciso que el conjunto factible esté acotado, es decir, que tenga un perímetro cerrado definido por las restricciones.

Considere el siguiente problema:

Max 5X₁ + 8X₂

Sujeto a:

6X₁ - 2X₂ ≥ 10

2X₁ + 8X₂ ≥ 20

Si traza las restricciones, observará que el conjunto factible no está limitado por la parte derecha, por tanto la función objetivo puede crecer de manera indefinida al tiempo que lo hacen X1 y X2, y no existe un máximo concreto. Hay un conjunto factible y también puntos extremos, pero la solución óptima es indeterminada.

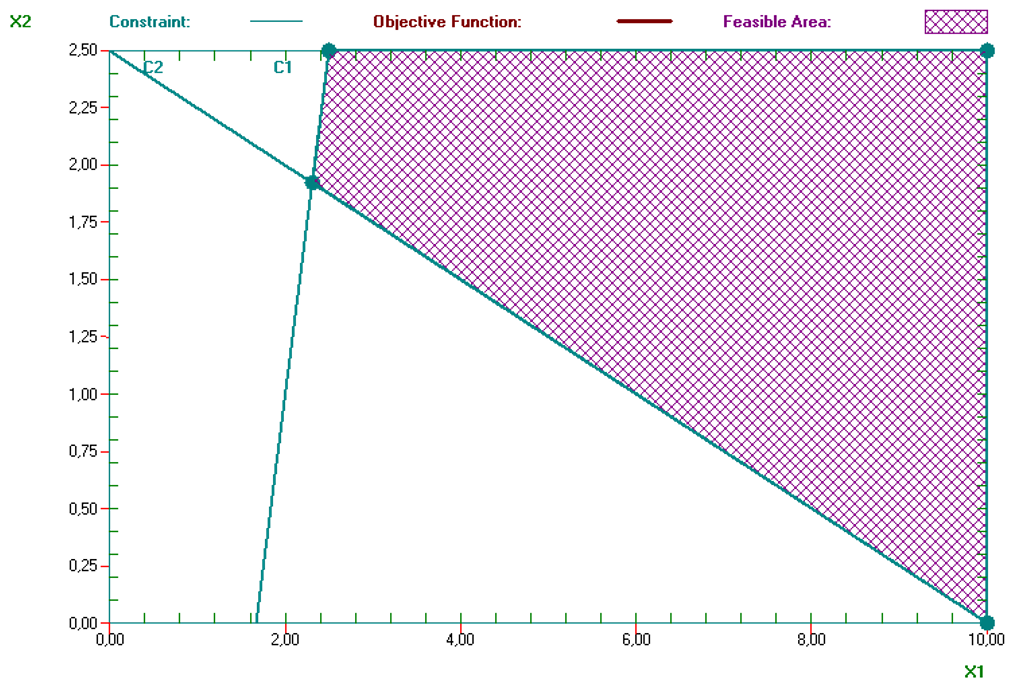
La causa habitual de este tipo de situaciones es la omisión de una o más restricciones relevantes en el problema.

En principio, cabe esperar que un programa lineal tenga muchas soluciones factibles, y una sola solución óptima. Pero en determinadas circunstancias, es posible que esa solución óptima pueda corresponderse con varias combinaciones de las variables de decisión, es decir: pueden existir varias soluciones óptimas, todas ellas con el mismo valor para la función objetivo.

Considere el siguiente programa:

Max. Z = X₁ + 4X₂

Sujeto a:

6X₁ - 2X₂ ≤ 8

2X₁ + 8X₂ ≥ 15

Podemos identificar la siguiente solución óptima (punto naranja):

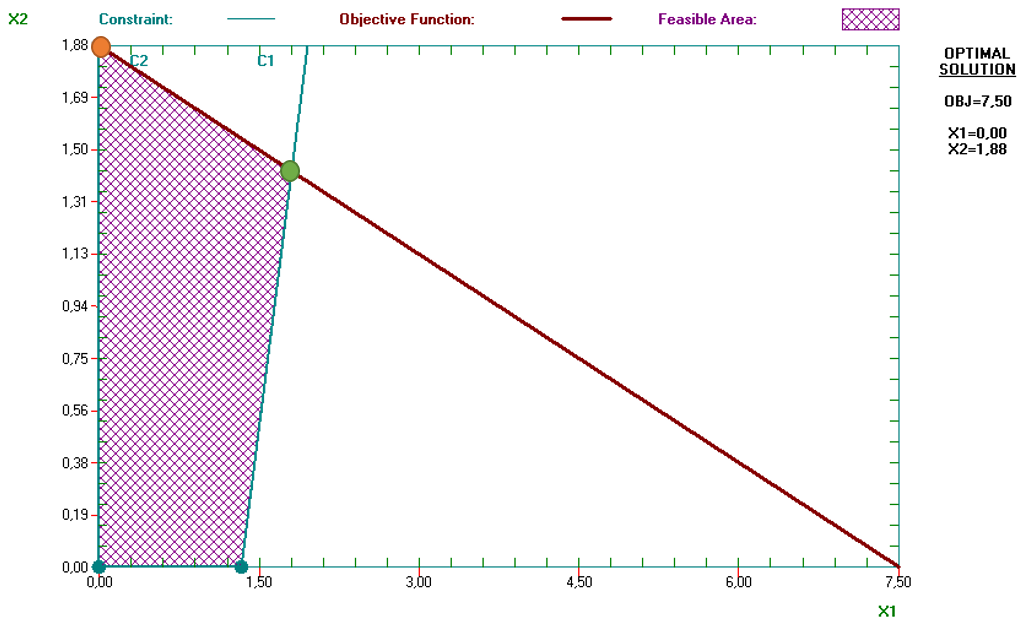
Pero puede comprobar que la combinación representada en verde devuelve el mismo valor para la función objetivo. Para identificarla basta con solucionar el siguiente sistema de ecuaciones:

6X₁ - 2X₂ = 8

2X₁ + 8X₂ = 15 ⇒ X1 = 1,81 y X2 = 1,42

La función objetivo toma el valor Z = X₁ + 4X₂ = 1,81 + 4 · 1,42 = 7,5, ¡precisamente el óptimo identificado más arriba!

En realidad obtendremos el mismo resultado para cualquier combinación situada sobre el segmento que une esos dos puntos extremos (naranja y verde): basta con calcular una combinación lineal convexa de ellos. Por ejemplo, la siguiente esta justo en la mitad de ese segmento (observe las ponderaciones):

X1' = 0,5 · 0 + 0,5 · 1,81 = 0,904

X2' = 0,5 · 1,875 + 0,5 · 1,42 = 1,649

donde la función objetivo toma exactamente el mismo valor: Z = X₁ + 4X₂ = 0,904 + 4 · 1,649 = 7,5 [para ganar precisión empleamos el valor óptimo de X2 sin redondeo, que es 1,875]

Cada una de esas combinaciones lineales da lugar a un nivel específico de producción de X1 y X2; sin embargo son indiferentes, en el sentido de que proporcionan el mismo valor (máximo) para la función objetivo y causan el mismo consumo de recursos.