Cuando las correlaciones toman valores realistas
En cualquier situación real las correlaciones entre los flujos de caja tomarán valores absolutamente dispares: no podemos esperar que sean perfectas, ni tampoco exactamente iguales a cero. Una forma de abordar esta situación es considerar las probabilidades condicionadas intertemporales, que expresan la verosimilitud de que ocurra un determinado evento (por ejemplo, que el flujo del período 1 tome un valor Q1 específico), supuesto que previamente ha ocurrido otro evento concreto (por ejemplo, que el desembolso inicial ha sido Go).
Aunque pueda parecer un planteamiento complejo, incluso engorroso, requiere menos información y es mucho más operativo que modelos formalizados como el de Hillier.
Manejando probabilidades condicionadas
Considere un proyecto que requiere un desembolso inicial de 500€ y puede proporcionar los siguientes flujos de caja:
- Desembolso inicial: 1.000€
- Q1 = 800 (con probabilidad del 40%) ó 600 (con probabilidad del 60%)
- Flujos del segundo período
- Si en t = 1 se percibieron 800€, en t = 2 se pueden obtener 800€ (con probabilidad del 70%) ó 400€
- Si en t = 1 se percibieron 600€, en t = 2 el flujo neto puede ser de 500€ ó 100€ (equiprobables)
El proyecto puede describirse mediante el siguiente gráfico
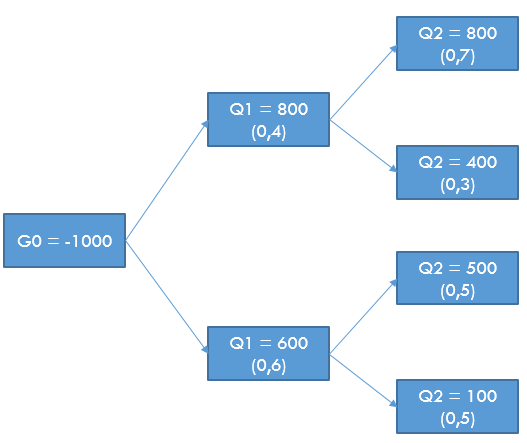
que expresa los valores posibles para los flujos de caja en cada período, considerando los eventos ocurridos en los anteriores, y las correspondientes probabilidades. Por ejemplo, Q2 podría ser igual a 800€ con probabilidad del 70%, pero solo si en t = 1 la tesorería neta ha sido 800€ (lo cual, a su vez, ocurrirá con una probabilidad del 40%). La probabilidad conjunta de que ocurran estos dos eventos es
P(Q1 = 800 ∩ Q2 = 800) = 0,4 · 0,7 = 0,28
y también puede estimarse, en virtud del Teorema de Bayes, como P(Q1 = 800 ∩ Q2 = 800) = P(Q1 = 800) · (PQ2 = 800 / Q1 = 800) siendo (PQ2 = 800 / Q1 = 800) la probabilidad condicionada de que el flujo en t = 2 sea 800€, supuesto que también ha sido de 800€ en t = 1.
Extendiendo este razonamiento al resto del grafo, podemos calcular las probabilidades conjuntas para los cuatro eventos finales; por supuesto, también los respectivos VAN:
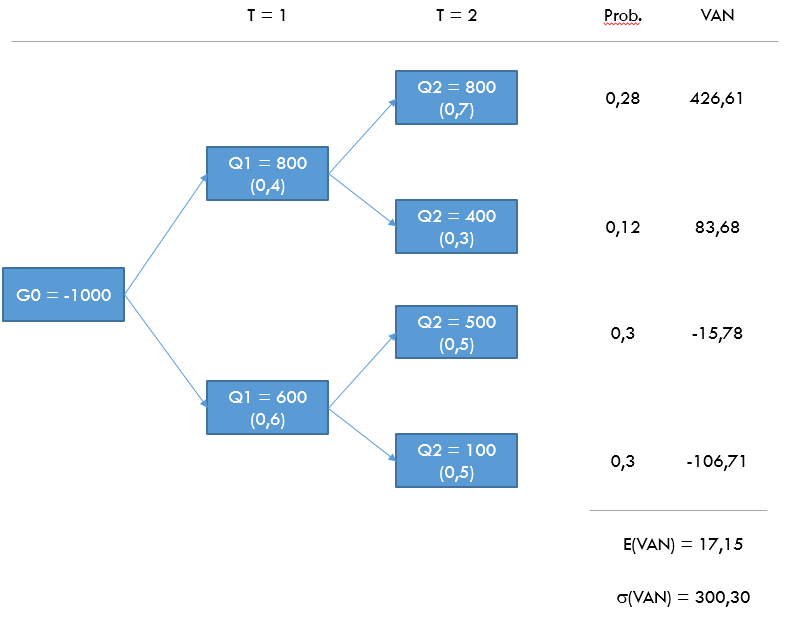
En el caso considerado más arriba (Q1 = Q2 = 800), el VAN esperado es -1000 + 800 · 1,08-1 + 800 · 1,08-2 = 426,61 y estimamos que esto ocurrirá con una probabilidad del 28%.
Si Q1 = 800 y Q2 = 400 el VAN será -1000 + 800 · 1,08-1 + 400 · 1,08-2 = 83,68; la probabilidad estimada de este evento es 0,4 · 0,3 = 0,12.
Una vez calculados los restantes valores y probabilidades, podemos estimar la esperanza matemática del VAN:
E(VAN) = 426,61 · 0,28 + 83,68 · 0,12 + (-15,87) · 0,3 + (-106,71) · 0,3 = 17,15
y el riesgo:
σ2(VAN) = 426,612 · 0,28 + 83,682 · 0,12 + (-15,87)2 · 0,3 + (-106,71)2 · 0,3 - 17,152 = 98,182,17
σ(VAN) = 98,182,171/2 = 300,30
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0