Árboles de decisión
Todos los modelos descritos hasta el momento asumen implícitamente que la elección de inversiones es un camino de una sola dirección sin salidas laterales: una vez adoptada la decisión, el proyecto se efectúa sin que exista posibilidad alguna de modificar su despliegue o su dimensión temporal. Al mismo tiempo el riesgo se concibe como una aleatoriedad genérica, con causas indeterminadas.
Sin embargo los proyectos reales son en mayor o menor medida flexibles. Incluso en las inversiones más complejas, suelen existir oportunidades para abandonar, para aplazar o demorar, para acelerar la ejecución, etc. La empresa puede desistir si el proyecto se desarrolla en condiciones adversas; desde luego esta decisión ocasionará un quebranto, pero los gestores tendrán siempre un margen de discrecionalidad para actuar.
Al mismo tiempo, las indeterminaciones suelen relacionarse con eventos o situaciones concretas. Quizá es el carácter imprevisible de la demanda lo que hace que no podamos anticipar con certeza los cobros; pero probablemente seremos capaces de esbozar escenarios y asignarles probabilidades siquiera subjetivas.
Finalmente, debemos considerar al tiempo como una variable relevante del problema. No es simplemente que los flujos de caja tengan una dimensión temporal, sino que las decisiones de la empresa pueden redistribuir esos flujos de caja (acelerando, aplazando, demorando, cancelando, etc. el proyecto); además, la exposición al riesgo no es igual durante la vida del proyecto: algunos eventos aleatorios ocurren en momentos concretos.
Los árboles de decisión proporcionan un poderoso instrumental para expresar la flexibilidad de la empresa (en forma de nodos decisionales) y los factores de riesgo (nodos aleatorios), todo dentro de una estructura con dimensión temporal.
Qué es un árbol, y cómo se evalúa
Un árbol es un tipo especial de grafo, conexo y acíclico, que estructura los distintos eventos que configuran un proyecto de acuerdo con condicionamientos temporales y analíticos. El árbol describe analíticamente el problema, identificando los posibles resultados y relacionándolos con el camino (la secuencia concreta de eventos) que los ha causado.
Que el grafo sea conexo significa que todos y cada uno de sus elementos (nodos) están vinculados con al menos otro; el árbol es acíclico en el sentido de que se diseña de acuerdo con la "flecha temporal" convencional, del presente hacia el futuro, y no admite retornos ni bucles (de manera formal, se dice que no tiene circuitos). Finalmente, la noción de condicionamiento hace referencia a que los nodos se estructuran de acuerdo con sus dependencias inherentes: si para elegir B tenemos que haber elegido antes A, el nodo correspondiente a B estará "después" del nodo correspondiente a A (vea el grafo más abajo); y no podremos alcanzar B si antes no hemos seguido el curso de acción A. De forma similar, si un evento aleatorio C puede producirse como consecuencia de haber elegido B, C estará "después" de B y, a su vez, "después" de A.
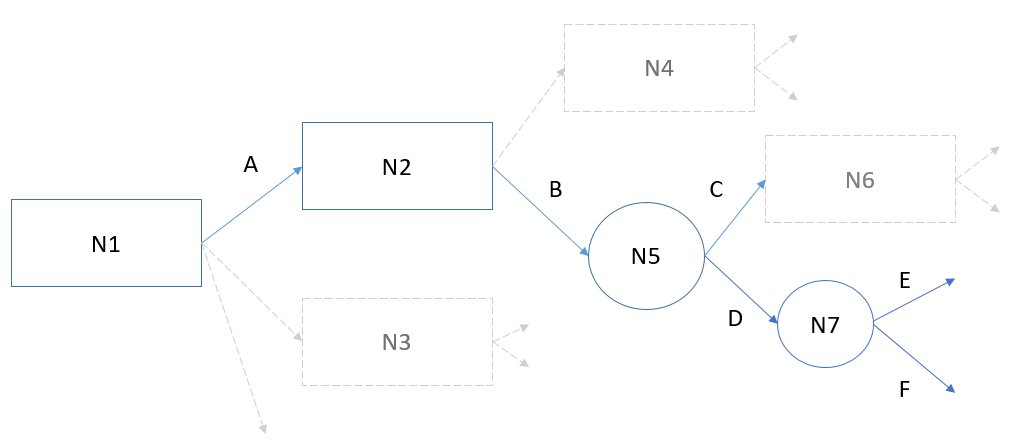
Como muestra la imagen inferior, un árbol se diseña combinando nodos y ramas. Cada nodo es un evento en el que o bien tomamos una decisión (nodo decisional, denotado con un cuadrado o rectángulo), o bien se produce un evento sometido a riesgo (nodo aleatorio, denotado con un círculo). De cada nodo parten dos o más ramas, que expresan las alternativas disponibles (nodos decisionales) o los estados que puede adoptar la naturaleza (nodos aleatorios). El árbol se lee de izquierda a derecha: ahora (N1) tenemos que adoptar una decisión eligiendo entre varias alternativas; si elegimos A más adelante deberemos adoptar una segunda decisión (N2) que a su vez nos conduce bien a una tercera elección (N4) o bien a un evento aleatorio (N5) que puede derivar en dos estados (C y D), uno de ellos conducente a una decisión (N6) y el segundo a otro fenómeno aleatorio (N7). Observe que el árbol estructura el problema en una secuencia temporal, desde el presente hacia el futuro.
Al final de cada uno de estos caminos tendremos un nodo terminal, que en el caso de las inversiones típicamente será un valor para el VAN.
 La evaluación del árbol es sencilla: en los nodos decisiones el decisor seleccionará la alternativa que ofrezca mayor valor esperado. En los nodos aleatorios estamos al albur de lo que ocurra en el entorno, sin embargo podemos calcular una esperanza matemática a partir de los valores terminales y de las probabilidades de cada uno de los eventos.
La evaluación del árbol es sencilla: en los nodos decisiones el decisor seleccionará la alternativa que ofrezca mayor valor esperado. En los nodos aleatorios estamos al albur de lo que ocurra en el entorno, sin embargo podemos calcular una esperanza matemática a partir de los valores terminales y de las probabilidades de cada uno de los eventos.
El Teorema de Bayes
Un aspecto especialmente atractivo de los árboles es la forma en que se combinan las probabilidades, ya que los distintos eventos dependen de, o están condicionados por los eventos que en su caso hayan ocurrido previamente. Por ejemplo la probabilidad de que en el nodo aleatorio N7 ocurra el evento E puede definirse como P(E); pero esta probabilidad está condicionada a que se hayan presentado las circunstancias necesarias para que la realidad llegue a ese nodo: el decisor debe haber elegido la alternativa A, después la B, y en N5 debe haber ocurrido el evento aleatorio D.
El evento E está condicionado por el evento D porque E puede ocurrir solo si antes ha ocurrido también D. En este sentido es relevante el Teorema de Bayes que, como probablemente sabrá, permite manejar probabilidades condicionadas; en particular, es útil para actualizar las probabilidades de ocurrencia de los eventos, a medida que se va conociendo nueva información del estado del entorno (en este caso, nueva información sobre lo que ha ocurrido en N5).
La probabilidad conjunta de que ocurra D y después E es P(D ∩ E) y, de acuerdo con el Teorema de Bayes, puede expresarse como
P(D ∩ E) = P(D) · P(E/D)
donde P(E/D) es la probabilidad de que ocurra E, supuesto que previamente ha ocurrido D. Lo realmente relevante es que los eventos no son independientes: sus probabilidades de ocurrencia están interrelacionadas, porque la ocurrencia (o no ocurrencia) de determinados eventos condiciona (hace posible o impide) que otros posteriores puedan llegar a presentarse.
Actividad
Cierta empresa, que actualmente se dedica a la reparación de calderas industriales, está considerando la posibilidad de ampliar su negocio a la venta e instalación de equipos nuevos.
Si iniciamos ahora este proyecto, tendremos que invertir 1.000€. Creemos que la demanda puede ser alta con una probabilidad del 60% y, en este caso percibiríamos unos flujos netos de caja de 2.000€ dentro de uno y dos años. Si, por el contrario, la demanda es baja los flujos netos en t = 1 caerán posiblemente hasta los 900€; en este caso la empresa podría abandonar el proyecto (recuperando, en t = 2, 200€ de la inversión inicial) o buscar un socio extranjero que ayude a abrir nuevos mercados y mejorar las ventas. En caso de hallarlo, los flujos netos de caja en t = 2 serían de unos 3.000€; por el contrario, si no se logra esta alianza, la facturación en t = 2 se situará en torno a 1.200€. Hemos estimado que la probabilidad de que las ventas sean bajas, y además no se halle un socio extranjero, es el 24%.
La empresa también puede aplazar la ejecución del proyecto hasta t = 1, para poder observar con más detalle el comportamiento de la demanda; en este caso la inversión inicial se reduciría hasta 700€. Creemos que en un 70% de los casos la demanda en t = 2 será bastante elevada, lo que proporcionará un flujo neto de caja de 1.700€ en t = 2; si la demanda resulta ser baja, el flujo neto en t = 2 se estima en 1.000€.
Vamos a evaluar el proyecto de ampliación, para un coste de capital del 10%.
Identificar y describir los nodos
Un nodo es un hito en el que, o bien tendremos que elegir entre varios cursos de acción, o bien se producirá un evento aleatorio.
En este caso podemos identificar los siguientes nodos:
- Decisionales
- Efectuar ya el proyecto, o esperar
- Si la demanda en t = 1 resulta ser baja, decidir si abandonamos o tratamos de aliarnos con un socio extranjero
- Aleatorios
- Demanda en t = 1, si decidimos efectuar ahora la inversión
- Demanda en t = 2, si decidimos esperar
- Existencia o no de un socio dispuesto a participar en el negocio, si efectuamos el proyecto y la demanda en t = 1 resulta ser baja
Observe que la propia definición de los nodos determina condicionamientos y una ordenación temporal.
Construir el grafo
El árbol se construye ordenando los nodos y trazando sus respectivas causalidades. Las reglas básicas son respetar la secuencia temporal y los condicionamientos lógicos inherentes al problema, garantizar que el grafo es conexo (y que, por tanto, no hay elementos aislados) y evitar bucles y circuitos (preservar la flecha temporal: del presente hacia el futuro).
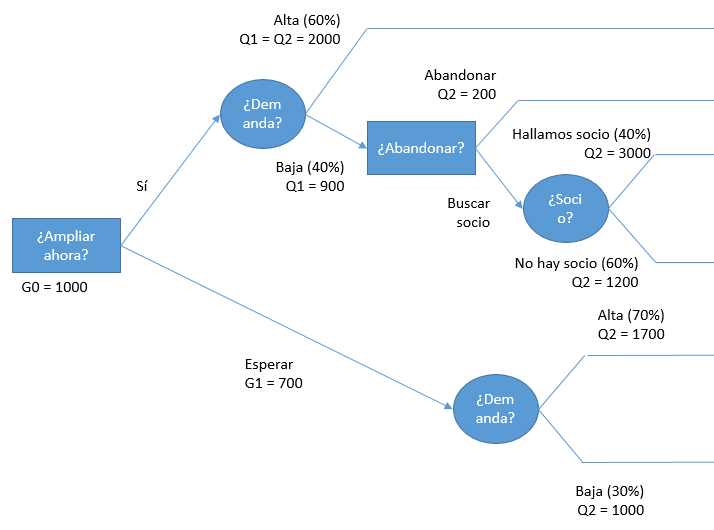
Además, se han añadido los flujos de caja y las probabilidades, en el caso de los nodos aleatorios. Todas ellas son conocidas, salvo la probabilidad de que (si la demanda en t = 1 ha sido baja, y hemos decidido no abandonar) en t = 2 no seamos capaces de hallar un socio extranjero. Sabemos i) que la probabilidad de que la demanda sea baja en t = 1 es 1 - 0,6 = 0,4; y ii) que la probabilidad conjunta de que las ventas sean bajas y además no se halle un socio extranjero, es el 24%. El Teorema de Bayes nos permite formular la siguiente igualdad:
P(baja en t = 1 ∩ no hallar socio en t = 2) = P(baja en t = 1) · P(no hallar socio en t = 2 / baja en t = 1)
0,24 = 0,4 · P(no hallar socio en t = 2 / baja en t = 1) ⇒P(no hallar socio en t = 2 / baja en t = 1) = 0,6
Evaluar los caminos
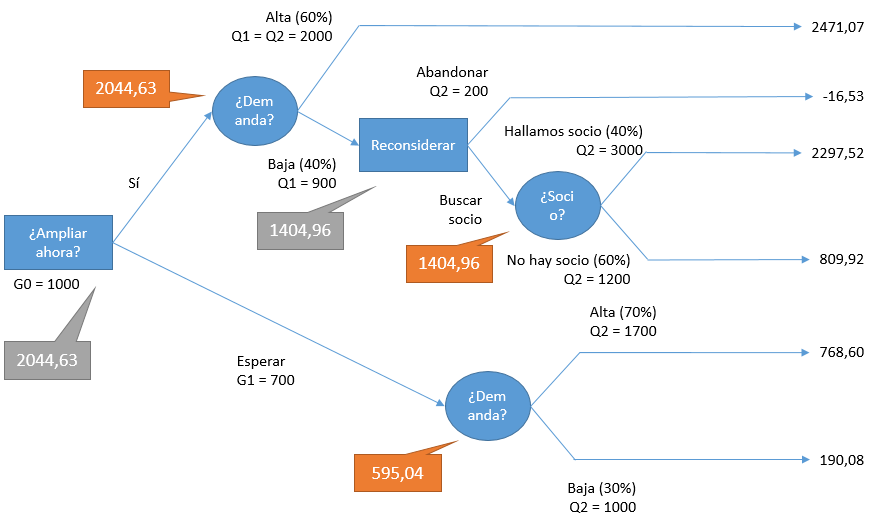
El diseño del árbol da lugar a seis caminos: seis posibles valores para el VAN, correspondientes a una secuencia específica de decisiones y eventos aleatorios.
El cálculo de estos valores es trivial. Considere en primer lugar que efectuamos ahora la inversión y la demanda resulta ser alta, de forma que desembolsamos ahora 1.000€ y percibimos 2.000€ anuales en t = 1 y t = 2:
VAN1 = -1.000 + 2.000 · 1,1-1 + 2.000 · 1,1-2 = 2.471,07€
Los restantes valores se calculan de la misma forma, con independencia de que atraviesen nodos aleatorios. Por ejemplo para el camino definido por Efectuar ahora > demanda baja > no abandonar > no hallar socio, se tiene:
VAN4 = -1.000 + 900 · 1,1-1 +1200 · 1,1-2 = 809,90€
Evaluar el árbol
Una vez conocidos los valores terminales, debemos evaluar el árbol. Para ello evaluamos los diferentes nodos desde el futuro hacia el presente, es decir, empezando por los más alejados en el tiempo y continuando después por los que los preceden, hasta llegar al nodo inicial.
Como señalamos, los nodos aleatorios se evalúan en términos de esperanza matemática; en los decisionales se selecciona el curso de acción con mayor valor esperado. El nodo aleatorio relativo a la búsqueda de un socio en t = 2 puede dar lugar a VAN3 = 2.297,52 con probabilidad del 40% ó a VAN4 = 809,92 con probabilidad del 60%; la esperanza matemática es
E(VAN) = 2.297,52 · 0,4 + 809,92 · 0,6 = 1.404,96€
de manera que en el nodo inmediatamente anterior (reconsiderar) el curso de acción más adecuado debería ser máx (-16,53; 1.404,96) = 1.404,96, es decir, tratar de hallar un socio. El nodo aleatorio precedente (demanda alta o baja) tendrá un valor esperado
E(VAN) = 0,6 · 2.471,07 + 0,4 · 1.404,96 = 2.044,63€
ya que esos son los valores correspondientes a cada una de sus ramificaciones (demanda alta o demanda baja). En la parte inferior del grafo, si la empresa decide esperar un año se enfrentará al carácter indeterminado de la demanda en t = 2, que tiene un VAN esperado de 595,04€. A la vista de todo ello la acción más adecuada ahora sería efectuar el proyecto, porque el VAN esperado de esta decisión (2.044,63€) es superior al VAN esperado de la alternativa de esperar (595,04€). Observe que estos cálculos incluyen no solo las diferencias en los desembolsos, sino también la heterogeneidad de los flujos de caja futuros, el tiempo, y las probabilidades estimadas de ocurrencia de los eventos aleatorios.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0