Precios sombra, holguras y rentabilidades marginales

Si ha trazado gráficamente las restricciones de los casos anteriores, probablemente habrá observado que su ubicación a derecha o izquierda depende del término independiente, y su pendiente del coeficiente técnico.

Cuando "relajamos" o flexibilizamos una restricción hacemos que se desplace hacia arriba y/o la derecha (si el límite aumenta) o hacia abajo y/o la izquierda (si el límite se reduce).

En el caso concreto que nos ocupa, cuando el límite de la primera restricción aumenta hasta 101 unidades, la restricción se desplaza hacia la derecha y el punto extremo correspondiente a la solución actual (E) se desliza a lo largo de la segunda restricción en la misma dirección hasta una nueva posición (H) que tiene como coordenadas A = 31,71 y B = 69,29. Anteriormente este punto no formaba parte de la solución factible, pero ahora sí, porque el desplazamiento de R1 ha ampliado el conjunto factible (ha añadido la franja oblicua sobreada en verde atenuado).

Este cambio hace que el valor (máximo) de la función objetivo aumente desde 405,72€ hasta 409,8€, es decir, una cantidad igual al precio sombra Ω1 = 4,14€.

Recuerde que los precios sombra valoran cambios marginales en los recursos; de esta forma se garantiza que la solución óptima se desliza a lo largo de las restricciones, y que permanecen las mismas variables (con diferentes valores). Si aplica cambios discretos es perfectamente posible que la solución "salte" a otro punto extremo, y en este caso la lógica matemática subyacente en el precio sombra no es aplicable.

Como hemos visto, cada precio sombra está asociado a una restricción, y cuantifica la variación que experimentará la función objetivo cuando el límite de esa restricción cambia, aumentando o reduciéndose en una unidad. El precio sombra mide la rentabilidad (o el coste) marginal de ese recurso.

Considere el factor X de nuestro ejemplo. El precio sombra asociado (Ω1 = 4,14) es diferente de cero porque la restricción original era activa, el inventario disponible de X estaba limitando real y efectivamente el programa productivo, y como acabamos de comprobar, disponer de cantidades adicionales permitiría mejorar el valor de la función objetivo. El precio sombra es el aumento de Z cuando X sufre un cambio infinitesimal; por tanto mide la rentabilidad marginal del factor X. También puede interpretarse como  el coste marginal de ese recurso: el lucro yacente que soportamos como consecuencia de que X esté limitado a 100 unidades, y el quebranto que sufriríamos si nos viésemos obligados a utilizar solo 99 unidades. Finalmente, es el precio máximo que podríamos estar dispuestos a pagar por la adquisición de una unidad más de ese recurso.

Hasta ahora únicamente nos hemos referido a programas consistentes en la optimización de la producción, condicionados por la disponibilidad de factores productivos. Pero, ¿y si hubiese restricciones relativas a otro tipo de recursos, por ejemplo financiación?

Vamos a ampliar nuestro modelo incorporando una restricción que limita la cantidad de dinero disponible para financiar el programa de producción. Supongamos que la producción de A ocasiona un coste total unitario de 0,5€ y que la producción de B tiene un coste total unitario de 0,2€; imaginemos además que tenemos un presupuesto limitado de 8€.

Nuestro modelo quedaría ahora planteado de la siguiente forma:

Max. Z = 2 · A + 5 · B

Sujeto a:

A + B ≤ 100

5 · A – 2 · B ≥ 20

0,5 · A + 0,2 · B ≤ 8

A ≥ 0

B ≥ 0

Naturalmente cabe esperar que la introducción de una restricción presupuestaria cambie la solución: es posible que no podamos efectuar el programa original con 8€, y también debemos considerar el hecho de que producir B es sustancialmente más barato que producir A.

Esta es la nueva solución óptima: A = 10; B = 15; Z = 95€. La nueva restricción (que en el gráfico se denota como C3) afecta severamente al programa porque una gran parte del conjunto factible original no respeta el presupuesto disponible; las soluciones viables ahora quedan limitadas al pequeño conjunto triangular que se muestra más abajo

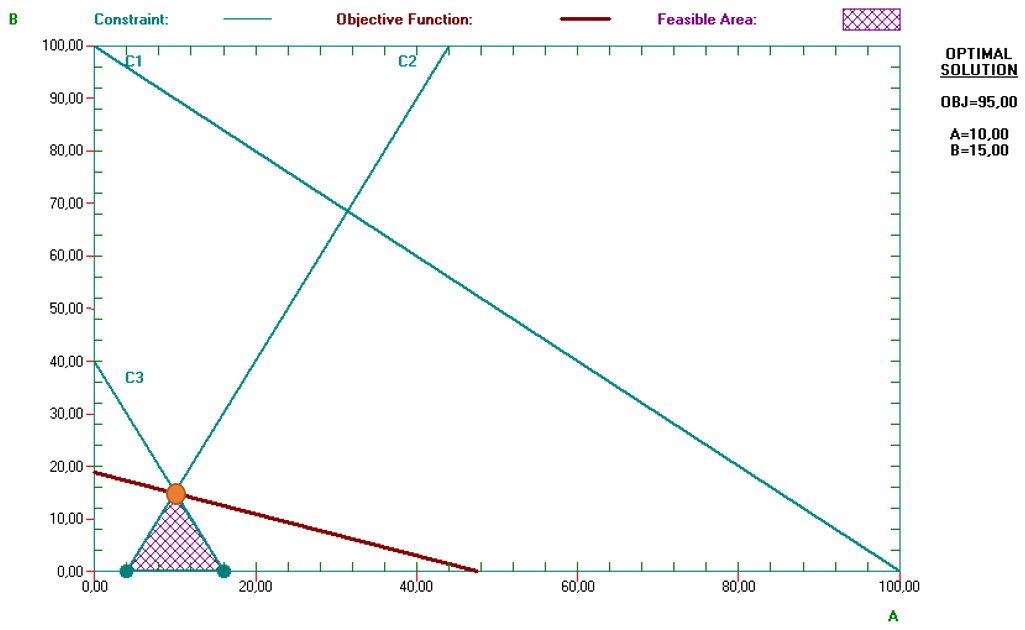
La restricción presupuestaria C3 es activa, y puede comprobar que su precio sombra es Ω3 = 14,5. Este valor tiene una interesante interpretación: es la rentabilidad marginal del capital. Si pudiésemos disponer de 1€ de financiación adicional, la función objetivo se incrementaría en 14,5€ (porque podríamos elaborar y vender más productos). Ganaríamos 14,5€ por euro adicional invertido en el ciclo productivo. En este caso la rentabilidad marginal es tan desproporcionada como poco realista; pero no hace sino poner de manifiesto el hecho de que la restricción financiera es muy intensa, mucho más severa que las limitaciones en la disponibilidad de factores productivos: la falta de presupuesto hace que solo podamos consumir 25 unidades del factor X y que otras 75 queden ociosas. La rentabilidad marginal está valorando esa necesidad perentoria de financiación adicional.

También puede interpretarse como un coste de oportunidad: es la cantidad de dinero que la empresa está dejando de obtener por el hecho de no disponer de más financiación. Las implicaciones son inmediatas: sin entrar en otras consideraciones, resultaría económicamente conveniente obtener financiación adicional y aplicarla al proceso productivo en la medida en que los desembolsos que ocasiona sean inferiores a 14,50€.