Caso propuesto
Vamos a analizar las diferentes posibilidades que tenemos para invertir en dos títulos (A, B) cotizados; en primer lugar calculamos los rendimientos históricos y obtenemos pronósticos de rendimiento y riesgo por extrapolación y empleando los respectivos modelos de mercado; analizamos la composición del riesgo, y finalmente formulamos los modelos de Markowitz y Sharpe.
Rendimientos históricos y pronósticos por extrapolación
Observamos durante cuatro días el comportamiento del precio de dos acciones (A, B) y del índice del mercado en el que cotizan ambos títulos. Los precios de cierre son los siguientes:
| Título A | Título B | Mercado | |
| Día 1 | 4 | 25 | 131 |
| Día 2 | 3 | 28 | 122 |
| Día 3 | 4 | 22 | 148 |
| Día 4 | 5 | 26 | 150 |
Vamos a estimar rendimientos por sesión, en este caso un rendimiento diario. A partir de esta serie (y permitiéndonos la licencia didáctica de tratar una serie tan corta), estimaremos la rentabilidad media y el riesgo históricos para el título A.
Más abajo se ofrecen dos hojas de cálculo para comprobar sus resultados o simular otros valores numéricos
¿Cuáles han sido las rentabilidades por período?
¿Qué rentabilidad, y qué riesgo, ha ocasionado el activo? ¿Qué valores podríamos esperar para la próxima sesión?
Analizando dos títulos
Como hemos anticipado, en el mercado se negocia también un título B, cuyos precios recientes se muestran más arriba.
Los rendimientos de los títulos A y B, ¿guardan algún tipo de relación?
La ecuación característica, o modelo de mercado
Continuando con los dos valores A y B considerados previamente, vamos a formular los correspondientes modelos de mercado
| Título A | Título B | Mercado | rAt | rBt | rMt | |
| Día 1 | 4 | 25 | 131 | |||
| Día 2 | 3 | 28 | 122 | -0,250 | 0,120 | -0,069 |
| Día 3 | 4 | 22 | 148 | 0,333 | -0,214 | 0,213 |
| Día 4 | 5 | 26 | 150 | 0,250 | 0,182 | 0,014 |
| Media | 0,111 | 0,029 | 0,053 | |||
| Varianza | 0,066 | 0,030 | 0,014 | |||
| Cuasivarianza | 0,100 | 0,045 | 0,021 | |||
| DT (poblac.) | 0,258 | 0,174 | 0,118 |
Pronósticos basados en el modelo de mercado
¿Cómo utilizaría la ecuación característica para formular pronósticos de rendimiento y riesgo?
Hoja de cálculo
¿Qué ocurriría si combinamos A y B en una cartera?
El resultado depende de las proporciones en las que se combinen A y B. Para comprobarlo, vamos a estimar el rendimiento y el riesgo de las carteras resultantes, para participaciones de A entre el 25% y el 100%.
Supongamos en primer lugar que xA = 0,75 y xB = 0,25. La cartera K resultante tiene el siguiente rendimiento esperado:
μK = 0,75 · 0,1111 + 0,25 · 0,0292 = 0,0906
El riesgo, medido por la varianza, será:
σ2K = 0,752 · 0,0664 + 0,252 · 0,0303 + 2 · 0,75 · 0,25 · (-0,0219) = 0,0310
| XA | XB | σ2K | σK | μK |
| 1 | 0 | 0,0664 | 0,2576 | 0,1111 |
| 0,75 | 0,25 | 0,031 | 0,1761 | 0,0906 |
| 0,5 | 0,5 | 0,0132 | 0,1149 | 0,0701 |
| 0,25 | 0,75 | 0,013 | 0,1139 | 0,0497 |
Es interesante observar que algunas carteras tienen un riesgo similar, pero rendimiento muy diferente (por ejemplo, las dos últimas combinaciones de la tabla anterior); también, que hay carteras con el mismo rendimiento pero diferente riesgo.
Como quiera que los decisores no son indiferentes ante la combinación de riesgo y rendimiento, se plantea la necesidad de identificar combinaciones eficientes, que maximizan el rendimiento para un nivel dado de riesgo (o, a sensu contrario, que minimizan el riesgo para un rendimiento específico).
Correlaciones, riesgo y diversificación
El riesgo de una cartera es la suma de la dispersión directa aportada por cada título (varianza) y del efecto indirecto que cada título causa sobre el riesgo de los demás (covarianza). Si combinamos dos títulos muy correlacionados obtendremos carteras muy volátiles, porque cada día, esos títulos tienden a obtener rendimientos similares, que se suman; dos títulos con correlaciones elevadas y negativas darán lugar a rendimientos que, con frecuencia, tendrán signo contrario y se compensarán mutuamente, de manera que la cartera tendrá un rendimiento medio mucho más estable.
Las correlaciones son un elemento determinante del riesgo de las carteras. Pero, ¿cómo influyen sobre las oportunidades de diversificación? ¿Es necesario que tengan signo negativo? ¿Qué ocurre cuando las correlaciones son positivas, que es la situación habitual en el mundo real?
¿Qué consecuencias se derivan de todo ello, desde el punto de vista de las posibilidades de optimización de carteras?
Gestionando el riesgo
Los rendimientos de A y B tienen correlación negativa; de hecho, los títulos tienen volatilidades de signo contrario.
¿Podríamos formar una cartera sin riesgo, combinando ambos títulos?
¿Podríamos formar una cartera libre de riesgo sistemático?
¿Y una cartera con un riesgo sistemático igual al del mercado?
Aplicando los modelos de mercado
Como los títulos individuales, las carteras tienen su propia ecuación característica, que podemos emplear para formular pronósticos de rendimiento y riesgo. Vamos a construir las estimaciones correspondientes a las carteras anteriores, partiendo de los estimadores de las ecuaciones de los títulos A y B:
| Título | αj | βj | σ2jε |
| A | 0,0183 | 1,7627 | 0,0229 |
| B | 0,0994 | -1,3346 | 0,0053 |
Optimización con el modelo de Markowitz
(los pronósticos de rendimiento y riesgo están basados en una extrapolación histórica. Ya sabe que existen otros procedimientos para establecerlos)
Las carteras resultantes de la resolución del modelo, para rendimientos esperados entre el 3% y el 11%, son las siguientes:
| XA | XB | σ2 | σ | μ |
| 0,010 | 0,990 | 0,029 | 0,171 | 0,030 |
| 0,132 | 0,868 | 0,019 | 0,138 | 0,040 |
| 0,254 | 0,746 | 0,013 | 0,113 | 0,050 |
| 0,376 | 0,624 | 0,011 | 0,104 | 0,060 |
| 0,498 | 0,502 | 0,013 | 0,115 | 0,070 |
| 0,620 | 0,380 | 0,020 | 0,140 | 0,080 |
| 0,742 | 0,258 | 0,030 | 0,174 | 0,090 |
| 0,864 | 0,136 | 0,045 | 0,212 | 0,100 |
| 0,986 | 0,014 | 0,064 | 0,253 | 0,110 |
Como era previsible, a medida que aumenta el rendimiento exigido a la inversión lo hace también la participación del tíutlo A, que es el que tiene mayor rentabilidad esperada (pero también más riesgo, de ahí que el modelo priorice la participación de B para niveles bajos de μK). No obstante, no debería tomar esto como una regla general, ya que en este caso estamos considerando solo dos activos que, además, tienen correlación negativa.
El gráfico inferior muestra la relación entre el riesgo, medido por la desviación típica, y el rendimiento esperado, para estas carteras diversificadas. Se sitúan a lo largo de una forma cuadrática, cuya rama inferior (en rojo) está dominada por la superior, que permite obtener un rendimiento superior para el mismo nivel de riesgo. Por ejemplo, podemos formar una cartera con un rendimiento esperado del 3% y un riesgo (medido por la desviación típica) del 17,10%; pero existe otra combinación que, con el mismo riesgo, permite aspirar a un rendimiento en torno al 9%.
La rama coloreada en verde es la frontera de carteras eficientes (FCE) del modelo de Markowitz, donde se sitúan las combinaciones que ofrecen la mejor expectativa de rendimiento, para un nivel dado de riesgo (o a sensu contrario, las combinaciones con menor riesgo, para un nivel dado de rentabilidad esperada).
El modelo de Sharpe
Hemos visto que también podemos pronosticar el rendimiento y el riesgo de los activos de capital empleando sus respectivas ecuaciones características. El modelo resultante, propuesto por Sharpe, permite simplificar sustancialmente los cálculos inherentes en el planteamiento de Markowitz al convertir la matriz de varianzas y covarianzas en una matriz diagonal unidad:
Estimamos la varianza de la perturbación aleatoria (σ2εj ) a través de la varianza de los errores de estimación.
Para el título A (cuyo modelo de mercado es rAt = 0,0183 + 1,7627 · rMt) se tiene que, σ2εA = SCEA / 3 = 0,0686 / 3 = 0,0229.
| rA | rMt | rAt* | eAt | eAt2 | |
| Día 1 | |||||
| Día 2 | -0,2500 | -0,0687 | -0,1028 | -0,1472 | 0,0217 |
| Día 3 | 0,3333 | 0,2131 | 0,3940 | -0,0606 | 0,0037 |
| Día 4 | 0,2500 | 0,0135 | 0,0421 | 0,2079 | 0,0432 |
| SCE(A) = | 0,0686 | ||||
| RE(A) = | 0,0229 |
Análogamente, σ2εB = SCEB / 3 = 0,0160 / 3 = 0,0053. El modelo de Sharpe queda como sigue:
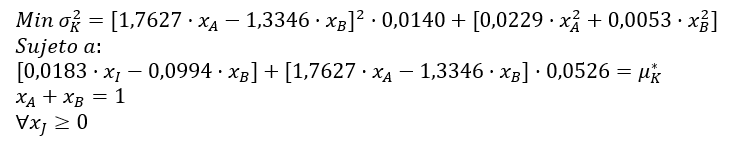
y su solución es nuevamente paramétrica, es decir: nos ayuda a identificar una cartera óptima para un nivel predeterminado de rendimiento esperado μK*.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0