¿Cómo tratar un programa lineal?
Nuestro primer programa lineal
Considere la siguiente situación: una empresa puede elaborar dos productos (X, Y) consumiendo otros tantos recursos (A, B) cuya disponibilidad es de 100 y 200 unidades respectivamente.
La tabla inferior recoge los márgenes y consumos unitarios:
| Producto | X | Y |
| Margen unitario | 2 | 4 |
| Consumo de A | 9 | 5 |
| Consumo de B | 10 | 50 |
de manera que cada unidad producida de X consume 9 unidades del recurso A y 10 del recurso B, y deja un margen neto de 2€. ¿Cómo deberíamos planificar la producción?
Sin entrar en otras consideraciones, podríamos dedicar la mayor cantidad posible de recursos a Y, que ofrece el margen unitario más alto; sin embargo también ocasiona un consumo desproporcionado del recurso B. El problema consiste en conciliar el interés económico con las restricciones técnicas.
Asumiendo solo por simplicidad que las cantidades producidas y vendidas son iguales, el margen del programa productivo será
Z = 2X + 4Y
de manera que formularemos la siguiente función objetivo:
Max Z = 2X + 4Y
No podemos producir cualquier cantidad de producto, porque estamos limitados por la disponibilidad de recursos. En concreto, el consumo del recurso A puede formularse como
9X + 5Y
y no puede superar las 100 unidades de que disponemos; por tanto nuestra primera restricción será
9X + 5Y ≤ 100
De forma similar, el consumo de B no puede superar las 200 unidades:
10X + 50Y ≤ 200
Nuestro problema se corresponde con el siguiente programa lineal:
Max Z = 2X + 4Y
Sujeto a:
9X + 5Y ≤ 100
10X + 50Y ≤ 200
(podemos añadir dos restricciones adicionales que impidan que X e Y tomen valores negativos, ya que son cantidades producidas y vendidas, aunque esta exigencia se asume por defecto).
Solución del programa, con software
Esta es la solución que proporciona Lindo, uno de los programas de investigacion operativa más comunes:
| Valor de la función objetivo: | 28 | |
| Variable | Valor | Coste reducido |
| X | 10 | 0 |
| Y | 2 | 0 |
| Restricción | Holgura | Precio sombra |
| 1 | 0 | 0,15 |
| 2 | 0 | 0,065 |
La solución óptima consiste en producir 10 unidades de X y 2 de Y, lo que proporciona un margen total de 28€. En efecto,
Z = 2X + 4Y = 2 · 10 + 4 · 2 = 28
Puede comprobar que este programa consume todos los recursos disponibles de A y B:
Recurso A: 9X + 5Y = 9 · 10 + 5 · 2 = 100
Recurso B: 10X + 50Y = 10 · 10 + 50 · 2 = 200
Como consecuencia, las holguras son iguales a cero. La holgura es la diferencia entre los términos derecho e izquierdo de cada restricción, en este caso la cuantía de recursos que no se consume.
Un resultado extraordinariamente importante son los precios sombra: sin entrar en detalles matemáticos, cada restricción tiene un precio sombra asociado que expresa el coste (o en su caso, la utilidad marginal) de ese recurso. Que el precio sombra de la primera restricción sea Ω1 = 0,15 significa que si pudiésemos disponer de una unidad más del factor A (101 unidades, en lugar de las 100 actuales) la solución se incrementaría en 0,15€, hasta 28 + 0,15 = 28,15€. Esto es así porque el factor A es actualmente restrictivo, en el sentido de que agotamos toda la cantidad disponible; si pudiésemos acceder a una unidad más podríamos producir X = 10,125 unidades e Y = 1,975 unidades, y lograr un margen de 28,15€. La diferencia es 28,15 - 28 = 0,15 = Ω1.
El cálculo de los precios sombra forma parte de la solución iterativa del programa; más adelante veremos un procedimiento para obtenerlos de forma sencilla, en el caso concreto de la selección de inversiones. Por el momento basta con razonar lo siguiente: disponer de una unidad más del recurso A es en principio valioso, porque actualmente lo estamos consumiendo por completo; podríamos aumentar la producción, siquiera en una pequeña proporción, y por tanto elevar el margen neto.
El precio sombra Ω1 es la rentabilidad marginal del factor A; también puede interpretarse como el coste máximo que podríamos admitir por la adquisición de esa unidad adicional de recurso.
Solución del programa con Excel o LibreOffice
Ambas hojas de cálculo incorporan una herramienta de optimización capaz de manejar programas restringidos: basta con diseñar el modelo de cálculo, dejándolo referenciado a dos celdas en las que estarían los valores de X e Y. Aplicando un algoritmo iterativo, la hoja nos devolverá la solución óptima y resultados adicionales, como las holguras y los precios sombra.
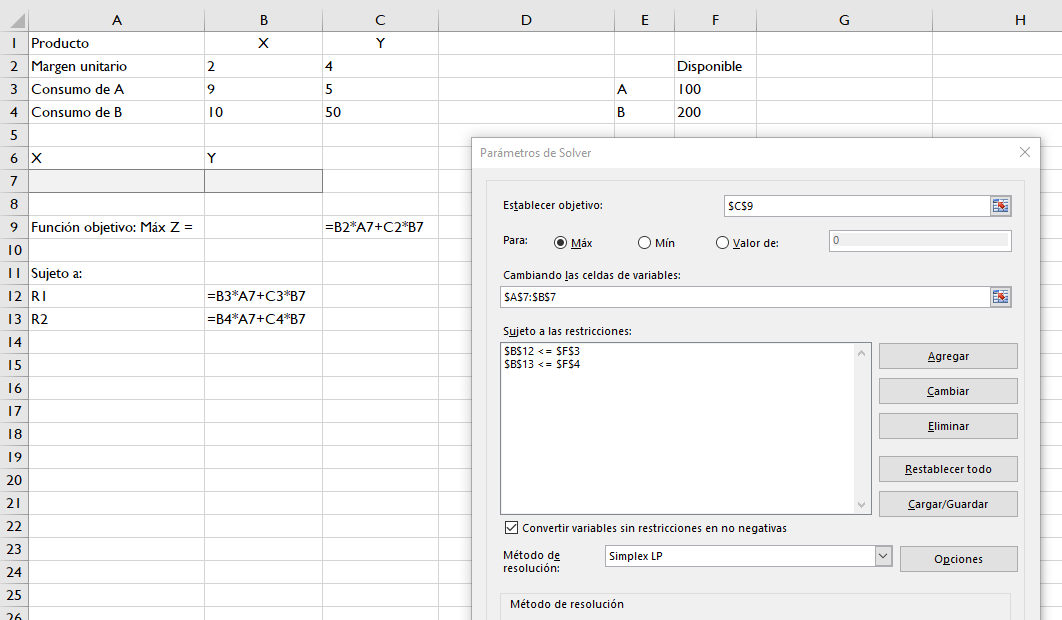
Recuerde que debe comprobar el contenido de la ventana de información que se le mostrará después de resolver el problema: asegúrese de que la hoja informa que ha encontrado una solución válida. En esta misma ventana puede solicitar un análisis de sensibilidad que le proporcionará, entre otros detalles, los precios sombra:
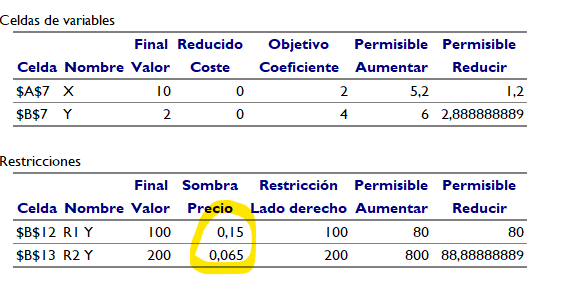
Solución del programa, de forma gráfica
La solución gráfica es viable solo cuando el problema tiene dos variables; pero resulta extraordinariamente ilustrativa, porque nos ayuda a comprender la manera en que operan las restricciones y a identificar la solución óptima sin necesidad de comprobar todas y cada una de las posibles combinaciones.
En primer lugar, trace gráficamente las dos restricciones; para ello basta con "despejar" Y (es decir, ponerla como función de X) y darle valores arbitrarios. Por ejemplo, la primera restricción puede formularse como
Y ≤ (100 - 9X) / 5
Obtenemos dos rectas (observe que las restricciones son lineales), cada una de las cuales da lugar a dos semiplanos a derecha e izquierda.
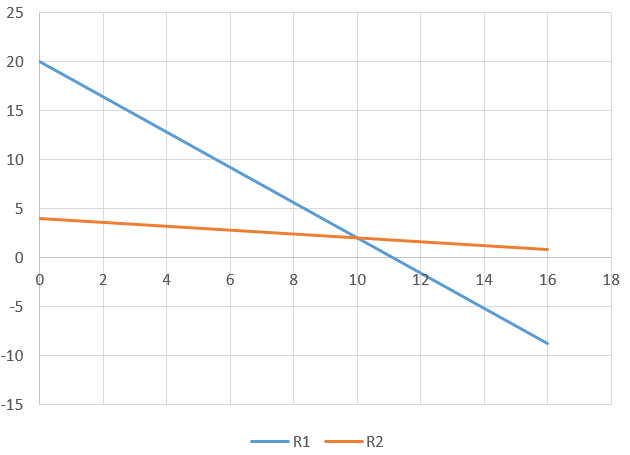
Considere ahora la primera restricción y dos puntos arbitrarios: (2, 5), en verde, y (10, 15) en naranja. La combinación (2,5) verifica la desigualdad porque 9X + 5Y = 9 ·2 + 5 · 5 = 43 < 100; es una combinación factible. Por el contrario (10, 15) no lo hace ya que 9X + 5Y = 9 ·10 + 5 · 15 = 165 > 100, es no factible. Puede comprobar que todas las combinaciones situadas por debajo de la línea recta verifican la desigualdad.
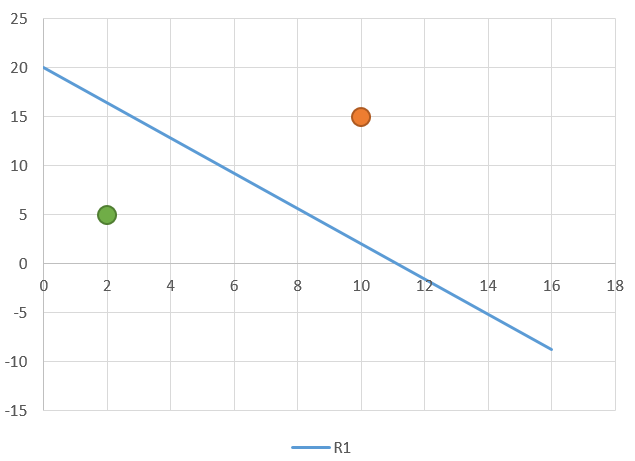
En el caso de la restricción 2 la situación es análoga: solo los puntos situados por debajo de ella cumplen la desigualdad.
Observe sin embargo que nuestro problema tiene dos restricciones, de forma que cualquier solución que queramos considerar debe verificarlas simultáneamente. El conjunto factible del problema son las combinaciones (X, Y) que cumplen ambas restricciones y, gráficamente, esto se corresponde con la zona de superposición de los dos semiplanos identificados más arriba.
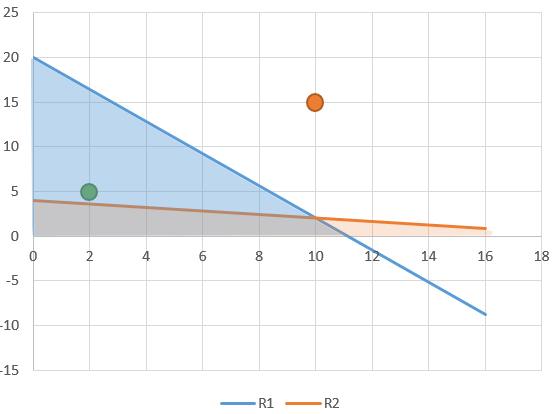
El punto (10, 15) no cumple la primera restricción (puede comprobar que tampoco cumple la segunda), de forma que descartamos los semiplanos superiores; el punto (2,5) cumple la primera restricción, sin embargo no cumple la segunda (está en el semiplano superior). Las combinaciones (X, Y) que cumplen ambas restricciones son las sombreadas en gris, delimitadas por las restricciones y los ejes de coordenadas (ya que no se admiten soluciones negativas); este es el conjunto factible del problema y la solución óptima está dentro de él.
Afortunadamente, tampoco tenemos que comprobar uno a uno todos los puntos del conjunto factible: puede demostrarse que la solución óptima, si existe, está en un punto extremo, es decir, en un vértice del conjunto factible. En nuestro caso estos puntos extremos son cuatro:
- La intersección de R2 con el eje de abscisas: (0, 4), donde la función objetivo vale 2 · 0 + 4 · 4 = 16
- La intersección de R1 con el eje de ordenadas: (11,11 0), donde la función objetivo vale 2 · 11,11 + 4 · 0 = 22,22
- La intersección de ambas restricciones: (10, 2) donde la función objetivo vale 2 · 10 + 4 · 2 = 28, que es la solución óptima del problema.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0