Casos de trabajo
Caso 1
Una empresa dispone de tres oportunidades para distribuir su presupuesto de capital, de 17€:
| Q0 | VAN | |
| A | -10 | 5,45 |
| B | -15 | 6,07 |
| C | -20 | -0,99 |
Ninguno de los proyectos puede efectuarse más de una vez
¿Cuál es el programa óptimo de inversión, sin los proyectos no son divisibles?
El modelo lineal en números enteros correspondiente a nuestro problema es el siguiente:
Para resolver el problema hemos de buscar un razonamiento que no haga necesaria la enumeración explícita de todas las soluciones factibles. Podemos pensar de la siguiente manera:
- El proyecto C es antieconómico y no condiciona a ninguno de los otros dos; por tanto, lo descartamos.
-
No podemos efectuar A y B simultáneamente - esto requeriría 25€ pero solo tenemos 17 -, de forma que hemos de optar por uno u otro
-
Si efectuamos A: VAN = 5,45€ y H1 = 7€ (este es el presupuesto ocioso)
-
Si efectuamos B: VAN = 6,07€ y H1 = 2€
-
-
Interesa efectuar B
-
Max VAN = 1 · 6,07 = 6,07€
-
Proyectos divisibles
¿Cómo cambia la situación, si los proyectos son perfectamente divisibles?
Si los proyectos son divisibles, podemos buscar una combinación de A y B que i) aproveche mejor el presupuesto disponible; y ii) incremente el valor de la función objetivo. El criterio de trabajo consiste en asignar fondos a los proyectos previamente ordenados de mayor a menor índice de rentabilidad (como se sabe, IR es la ratio entre el VAN del proyecto y el desembolso inicial, por tanto es una medida del valor medio aportado por cada euro invertido). Aplicamos una estrategia de saturación, es decir, asignamos fondos hasta alcanzar el límite de una o más de las restricciones del problema (financiera o técnica).
En este caso procedemos de la siguiente manera:
- Calculamos los índices de rentabilidad: IRA = 5,45 / 10 = 0,55; IRB = 6,07 / 15 = 0,40
- Asignamos fondos al proyecto A hasta agotar el presupuesto o, en su defecto, saturar la restricción técnica XA ≤ 1.
- Efectuamos A una vez, invirtiendo 10€; restan 7€ que se asignan al proyecto B, el cual se efectúa en 7/15 partes
- La solución óptima es (A,B) = (1 7/15)
- El VAN de la cartera de proyectos es 1 · 5,45 + (7/15) · 6,07 = 8,28€.
- La restricción financiera es activa (invertimos 17€, por tanto la holgura es nula); también es activa la restricción XA ≤ 1; la última restricción (XB ≤ 1) es inactiva, ya que el prpoyecto B no llega a efectuarse por completo por falta de financiación.
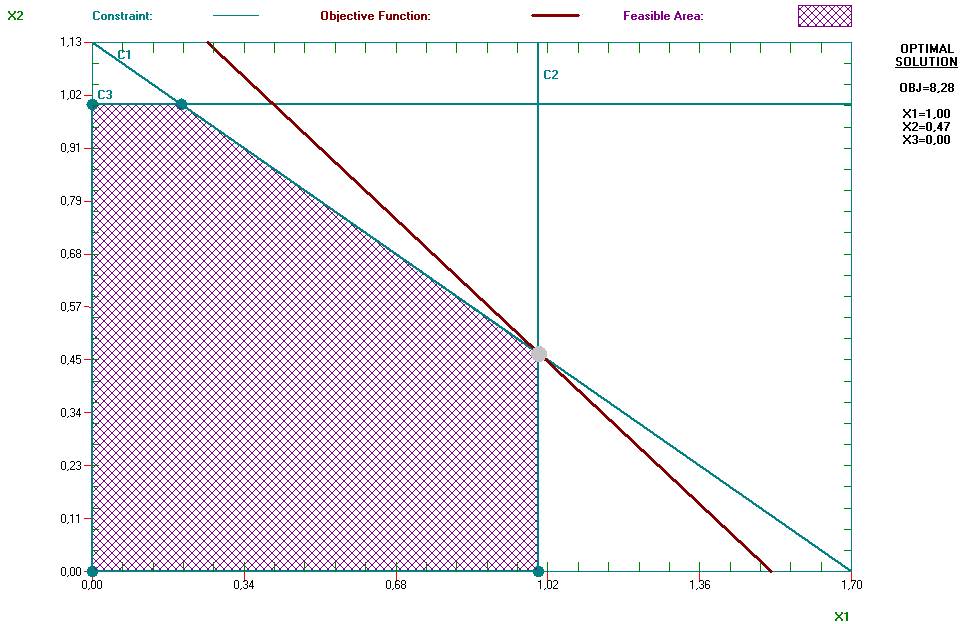
Este es un resumen de la solución:
Precios sombra y marginalidad
¿Qué puede decir de los precios sombra del programa de inversión?
El teorema de la holgura complementaria (THC) garantiza que:
- En el caso de las restricciones con holgura (inactivas), el precio sombra correspondiente es cero
- Si el precio sombra es diferente de cero, la restricción es activa
Por tanto, solo podemos afirmar que el precio sombra correspondiente a XB≤1 es cero. Dada la configuración del problema, es posible que los precios sombra de las restricciones 1 y 2 sean positivos, pero el THC no lo garantiza. Para calcularlos podemos preguntarnos qué ocurriría si nuestro presupuesto se incrementase en una pequeña cuantía, digamos 1€; es decir,cómo cambiaría el programa de inversión, si dispusiésemos de 17 + 1 = 18€?
- Efectuamos A hasta el límite (XA' = 1)
- Efectuamos B en (7+1) / 15
- El valor de la función objetivo aumenta hasta VAN' = 1 · 5,45 + (8/15) · 6,07 = 8,69
- La solución anterior era VAN = 8,28; por tanto ΔZ = 8,69 – 8,28 = 0,41 = Ω1
El precio sombra de la primera restricción, expresivo del coste de oportunidad del dinero en t = 0, es igual al 41%: si la empresa pudiese incrementar su presupuesto en 1€ modificaría oportunamente su programa de inversiones, y esto se traduciría en un aumento de 41 céntimos en el VAN; en otras palabras, la rentabilidad marginal del dinero es el 41%.
De la misma forma podemos anticipar que, si la empresa tuviese que reducir su presupuesto en 1€, el VAN de la cartera de proyectos se reduciría en 0,41€.
Precio sombra de la restricción financiera
Cuando aumentamos el presupuesto la restricción financiera se desplaza hacia la derecha; esto ensancha la zona factible, haciendo viables soluciones que antes no podíamos alcanzar porque superaban la financiación disponible. En nuestro caso, un aumento del presupuesto permite abordar todas las combinaciones situadas en la franja naranja mostrada en el gráfico inferior; la solución óptima se desplaza hacia arriba, a lo largo de la restricción XA≤1, hasta alcanzar la intersección con la restricción financiera (recuerde que la solución óptima siempre se halla en un punto extremo de la zona factible). La solución inicial está señalada en azul, la nueva solución en rojo.
Precio sombra de las restricciones técnicas
Si pudiésemos efectuar el proyecto B más de una vez la solución no cambiaría, porque en las condiciones actuales no disponemos de financiación para efectuarlo siquiera una sola vez.
La situación con el proyecto A es, sin embargo, muy distinta: la posibilidad de efectuar A más de una vez es económicamente atractiva porque este proyecto tiene IRA = 0,55 (frente a IRB = 0,40); por tanto, cada euro destinado a B implica un lucro yacente de 0,15€. Supongamos que pudiésemos efectuar A hasta un máximo de 1,5 veces (por tanto, XA≤1,5): efectuaríamos A 1,5 veces (consumiendo 1,5 · 10 = 15€); los otros 2€ se destinarían a B, que se efectuaría en 2/15 partes. El VAN aumenta en 0,7023 de manera que el precio sombra correspondiente a la segunda restricción es 0,7023 / 0,5 = 1,4033.
Observe que los precios sombra evalúan el impacto económico de un cambio unitario en el límite de la restricción:; cuando simulamos cambios de cuantía inferior, nuestros cálculos muestran una variación también proporcionalmente inferior.
En este caso, la restricción técnica XA≤1 se desplaza hacia la derecha, ampliando el conjunto factible con el polígono sombreado en amarillo; como el proyecto A es económicamente más deseable, se prioriza su ejecución hasta el nuevo límite de la restricción, destinando el resto del presupuesto al proyecto B.
Análisis de sensibilidad
¿Qué cambios podría experimentar VANA, de forma que el programa de inversión permanezca inalterado?
Una limitación importante del enfoque de racionamiento es la ausencia de un tratamiento específico del riesgo.
Una forma de superar este condicionante, e intuiir el grado de estabilidad de la solución, es simular el comportamiento del programa cuando se modifica alguno de sus parámetros; esto es lo que hacemos al calcular los precios sombra, y podemos formular cálculos similares también para los coeficientes técnicos y directos del modelo. Una de las variables más significativas en este sentido es el VAN (el coeficiente de valor directo del proyecto), en que subsume los flujos de caja y el coste de capital.
El proyecto A es el que se efectúa en primer lugar:
- Su VAN podría crecer de forma ilimitada, sin que la clasificación de los proyectos cambie. La solución seguirá siendo la misma, aunque su valor económico aumentará con VANA.
- El VAN del proyecto A podría reducirse hasta que IRA = IRB; si VANA sigue cayendo tendríamos IRA < IRB de forma que el proyecto B tendría prioridad y la solución cambiaría. Se trata por tanto de que se verifique la siguiente desigualdad:
de manera que la clasificación (y la solución) se mantienen en tanto VANA > 4; la reducción máxima admisible en VANA sería 5,45 – 4 = 1,45€.
Cambios en las restricciones
¿Qué ocurriría si se impone una nueva restricción 2XA + 7XB + 10XC ≤ 40?
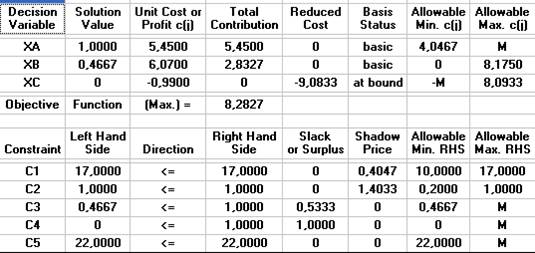
La solución actual (1 0,47) verifica esta restricción ya que 2XA+7XB+10XC = 2 · 1 + 7 · 0,47 + 10 · 0 = 5,29 < 40. La restricción no es activa, por tanto no ejerce ninguna limitación efectiva sobre la solución, y el programa òptimo no cambia.
En el gráfico inferior puede observarse que la nueva restricción (en trazo verde grueso) está muy alejada de la zona factible, lo que indica no solo que es inactiva, sino también que su holgura es amplia.
¿Qué ocurriría si se impone la siguiente nueva restricción: 15XA + 15XB + 20XC ≤ 22 ?
Esta restricción se cumple en términos de igualdad: en efecto, 15XA + 15XB + 20XC = 15 · 1 + 15 · 0,47 + 20 · 0 = 22. Por tanto no tiene holgura y es activa, aunque no modifica la solución.
Sin embargo el análisis de la solución arroja un curioso resultado: aún siendo activa, esta restricción tiene un precio sombra igual a cero. Recuerde que el THC garantiza que las restricciones con precio sombra no nulo son activas, pero que el inverso no se cumple necesariamente. Aquí tenemos una restricción que se cumple en términos de igualdad pero lleva asociado un precio sombra cero: aunque modificásemos el límite de esta restricción, la solución no cambiaría en absoluto. ¿Cómo es esto posible?
Para comprenderlo es útil recurrir a la representación gráfica de las restricciones y la zona factible. Como puede comprobar en el gráfico superior, esta restricción se intersecta con la restricción financiera inicial, precisamente, en el punto correspondiente a la solución. Esto significa que, aunque desplazásemos a la derecha la nueva restricción, la solución seguiría estando limitada por la restricción financiera inicial y por la técnica XA≤1, es decir: en este caso, cambiar una sola restricción no permite mejorar la solución, sería preciso alterar dos o más restricciones, de ahí que el precio sombra sea cero.
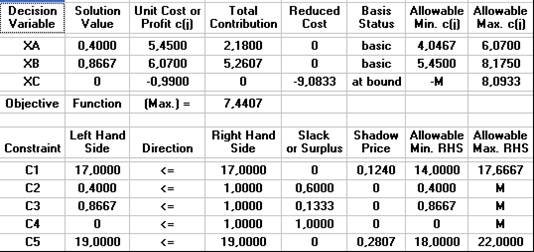
¿Qué ocurriría si se impone la siguiente nueva restricción: 15XA + 15XB + 20XC ≤ 19 ?
Resulta evidente que la solución en curso no verifica esta restricción, por tanto la solución óptima va a cambiar. La incorporación de la nueva restricción hace que una parte de la zona factible deje de verificar el nuevo sistema de limitaciones, y en este caso ocurre que el punto extremo de la solución óptima está precisamente en esa zona (sombreada en amarillo, en el gráfico inferior).
Como veremos en el siguiente apartado, la nueva solución depende del valor de los índices de rentabilidad de los proyectos, en cada período.
| A | B | C | Lím | |
| VAN | 5,45 | 6,07 | -0,99 | |
| R1 | 10 | 15 | 20 | 17 |
| R2 | 15 | 15 | 20 | 19 |
| IR1 | 0,55 | 0,4 | -0,05 | |
| IR2 | 0,36 | 0,4 | -0,05 |
Cuando, como en este caso, un proyecto aventaja al otro en un período, pero no en los restantes, la solución consiste en un programa mixto de ambas inversiones; geométricamente, la solución se corresponde con el punto en el que se intersectan las dos restricciones financieras. Por tanto, basta con resolver el siguiente sistema de ecuaciones:
10XA+15XB+20XC=17
15XA+15XB+20XC=19 → XA = 0,4 y XB = 0,8667
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0